Lecturer: Dr Stephen Millmore and Dr Nandan Gokhale
This course extends the validity of the models covered in Numerical Methods for Compressible Fluid Dynamics to cover all four standard states of matter. This requires the role of the equation of state in governing the underlying thermodynamic properties of different materials to be studied. The magnetohydrodynamic effects of modelling plasma, and the deformation gradient and strain requirements for modelling solids, are covered to enable this generalisation of the underlying models. Additionally, further consideration is given to mesh generation, and how boundaries can be introduced into the computational domain whilst retaining the ability to use numerical and discretisation procedures suitable for non-linear compressible systems of equations. Through the practicals, students will be able to extend their existing work such that they can simulate various materials, culminating in writing their own magnetohydrodynamics solver. This course combines physics and mathematics, and is suitable for students with a background in either of these areas, including engineering.
Students should leave the course knowing:
- How to write code for simulating gases, liquids, solids and plasma
- How Maxwell’s equations combine with the Euler equations to give the equations of magnetohydrodynamics
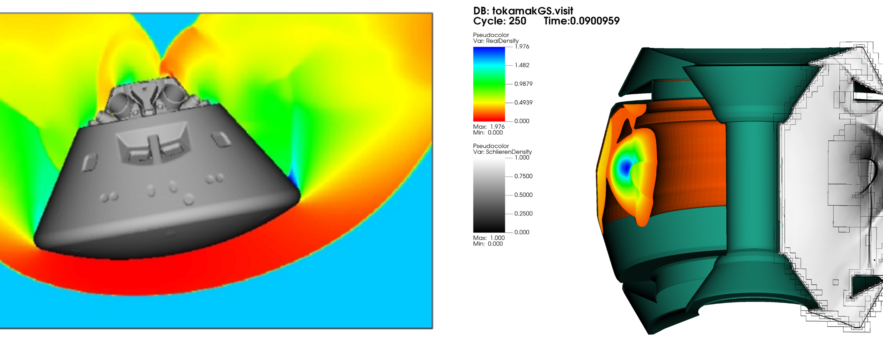
- How cut cell methods can be used to incorporate arbitrarily complex geometries within a simulation
Lectures:
- Mesh generation for continuum modelling (Part 1) (Dr N. Gokhale)
Overview of grid generation techniques; comparison of different mesh types; introduction to cut cell methods; meshing from STL files - Mesh generation for continuum modelling (Part 2) (Dr N. Gokhale)
Geometric information in cut cell methods; the small cell problem and cut cell approaches; the flux stabilisation cut cell method; convergence properties of cut cell methods - Source terms and equations of state (Part 1)
Including body forces and other source terms in hyperbolic systems of equations; simple coordinate transformations; derivation of the ideal gas equation of state; mathematical quantities for an equation of state - Equations of state (Part 2) and magnetohydrodynamics (Part 1)
Equations of state for gases, liquids and solids; reference quantities for defining material properties; tabulated equations of state; modelling a plasma; combining Maxwell’s equations with the Euler equations - Magnetohydrodynamics (Part 2)
Mathematical properties of the magnetohydrodynamics equations (MHD); numerical methods for MHD; the divergence constraint; from ideal to resistive MHD; MHD for simulating lightning - Elastoplastic solids
Compressible models for simulating solids; stress, strain and strength; high strain-rate behaviour; evolution equations for an elastoplastic solid; separating elastic and plastic effects
Practicals:
All practicals require students to write their own code, typically in C++, in which demonstrators will be familiar, though other languages may be used.
- Two-dimensional Euler equations (Part 1)
Modification of one-dimensional schemes to work in two dimensions, with application to multi-dimensional problems - Two-dimensional Euler equations (Part 2)
Continuation of the first practical - Geometric source terms
Allowing one-dimensional codes to run for cylindrical and spherical symmetry, and two-dimensional codes to run in cylindrical symmetry, comparing to results from previous practicals - Beyond the ideal equation of state
Simulating problems with the stiffened gas equation of state for shocked water, and a Mie-Grüneisen equation of state for a high-speed solid - Magnetohydrodynamics (Part 1)
Developing a code to solve for one-dimensional MHD problems, with the simulation of multi-wave shock tube tests - Magnetohydrodynamics (Part 2)
Continuation of the previous practical
Prerequisites:
- Scientific Programming in C++ (or other C++ courses)
- Numerical Methods for Compressible Fluid Dynamics
Required course for:
- Multiphysics Modelling for Four States of Matter
Recommended reading:
- Toro, Eleuterio F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction. Springer Science & Business Media, 2013.
- Goedbloed, JP Hans, J. P. Goedbloed, and Stefaan Poedts. Principles of magnetohydrodynamics: with applications to laboratory and astrophysical plasmas. Cambridge university press, 2004.
- Hiermaier, Stefan. Structures under crash and impact: continuum mechanics, discretization and experimental characterization. Springer Science & Business Media, 2007.
Picture credit:
- Nandan Gokhale
- Alexis Farmakalides